Chris Greening

Chris Greening

Software engineer particularly fond of Python and R

In the world of mathematics there is a limitless supply of patterns, visualizations, and concepts just waiting to be explored

A particularly interesting set of concepts are known as hypotrochoids and epitrochoids - beautiful patterns traced by a point extending from a circle rolling around another fixed circle

Pattern drawn from a hypotrochoid

Let’s dive in and explore how spyrograph helps us analyze and explore these interesting mathematical concepts in just a few lines of code!

What are hypotrochoids and epitrochoids?

Simply put, hypotrochoids and epitrochoids are curves formed by tracing a point extending from the center of a circle as it rolls around the inside (for a hypotrochoid) or the outside (for an epitrochoid) of a fixed circle

Circle rolling around the exterior of a fixed circle and drawing a looping pattern

The resulting curves can be incredibly intricate, elegant, and pleasing to the eye and have a surprisingly wide range of applications ranging from engineering and astronomy to even patterns printed on banknotes and passports as security measures against counterfeiting

Exploring the math behind these patterns

Hypotrochoids and epitrochoids can be broken down to a few key inputs and a set of parametric equations

The inputs are:

  • \(R\): the radius of the fixed circle
  • \(r\): the radius of the rolling circle
  • \(d\): the distance from the interior of the rolling circle
  • \(\theta\): the angle formed by the horizontal and the center of the rolling circle

with the parametric equations defined as:

Hypotrochoid

\(x(\theta) = (R - r)cos\theta + d cos(\frac{R - r}{r}\theta)\) \(y(\theta) = (R - r)sin\theta - d sin(\frac{R - r}{r}\theta)\)

Epitrochoid

\(x(\theta) = (R + r)cos\theta - d cos(\frac{R + r}{r}\theta)\) \(y(\theta) = (R + r)sin\theta - d sin(\frac{R + r}{r}\theta)\)

Given this information, we can draw our curves using the output \((x,y)\) coordinates calculated by the parametric equations

Drawing of a hypotrochoid plot

Installing spyrograph

Getting spyrograph installed and ready to go is as easy as installing the latest stable release from PyPI or cloning the development version from the official GitHub repo

PyPI

pip3 install spyrograph

GitHub

git clone https://github.com/chris-greening/spyrograph.git

No additional configurations or third-party libraries necessary to get started; spyrograph leverages the Python standard library with optional support for pandas and matplotlib

Using spyrograph for effortless modeling

The purpose of spyrograph is to take the parametric equations and build them into an expressive, easy-to-use set of tools for quickly modelling, exploring, and visualizing the behavior of these curves in Python

from spyrograph import Hypotrochoid
import numpy as np

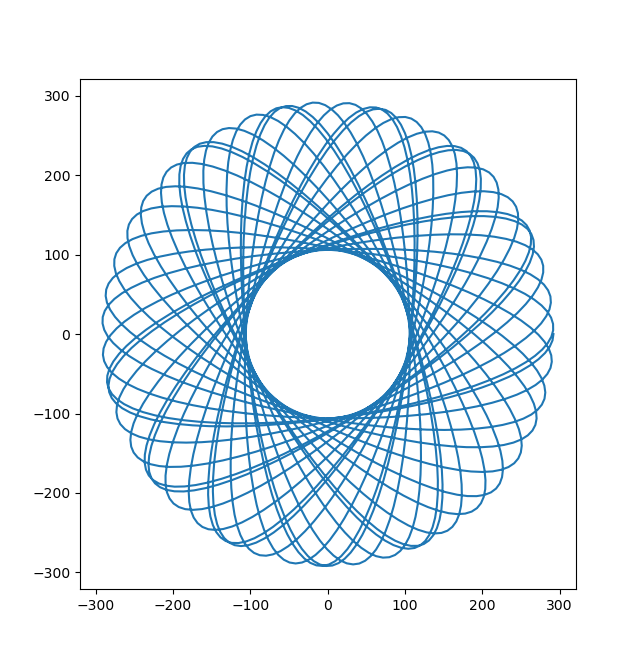
hypotrochoid = Hypotrochoid(
    R=423,
    r=203,
    d=101,
    thetas=np.arange(0, 720, .1)
)
hypotrochoid.trace()

Drawing of a hypotrochoid plot shaped like a donut with many intersecting lines and patterns

With just our input parameters and a couple lines of code, we can get on our way tracing our curves and generating stunning visualizations letting spyrograph abstract away the underlying math and implementation details

On top of hypotrochoids and epitrochoids, we also define special cases of these curves such as the

  • Hypocycloid
  • Epicycloid
  • Deltoid
  • and the Astroid

for explicit, object-oriented models that are clean, flexible, and ready for programming against

Conclusion

And just like that we can draw beautiful, complex patterns and shapes letting spyrograph deal with all the math and visualization boilerplate

Just plug-and-play your parameters and start exploring the beautifiul world of math!

Additional references

Updated:

You May Also Enjoy